What kinds of input data can be used for generating forest stand structure in the growth simulator SIBYLA?
The growth simulator SIBYLA can generate information about individual trees from different data sources as described in Table 1.
Table 1 Possible input data for generating forest structure including their information sources
| nature of input data | information source |
| 1. Tree data |
|
| 2. Frequency data: diameter - height - quality |
|
| 3. Frequency data: diameter - height |
|
| 4. Frequency data: diameter - quality |
|
| 5. Frequency data: diameter |
|
| 6. Stand data |
|
| 7. Yield tables |
|
| 8. Parameters of selection forest |
|
The precision of generating forest stand structure decreases as the level of detail of input data is reduced, i.e. in the direction from the top to the bottom in the above table.
How is forest stand structure of the type of age classes generated?
A forest of a type of age classes is a forest that is managed by currently the most common management forms, i.e. it is a forest that originates from the regeneration of the continuous smaller and larger plots. The plots occur after the deforestation following the regeneration felling or compartment disturbance, on which artificial reforestation combined with occurring natural regeneration next to the parent stand is used. The plots can also originate from a substantial thinning caused by prescribed cutting, e.g. when applying the shelterwood silvicultural system, or from scattered salvage cutting. In such cases, underplanting or natural regeneration below the parent stand is used. In either of the cases, the final forest is composed of the trees that belong to one age class (in the range of 20 years) found over the whole stand area and belonging to one stand layer (storey). Even-aged homogeneous and mixed forest stands, as well as multi-storied forests and high-forests-with-reserves including plantation forests fall into this category. In this case, the data of type 1 to 7 from Table 1 can be used as input data.
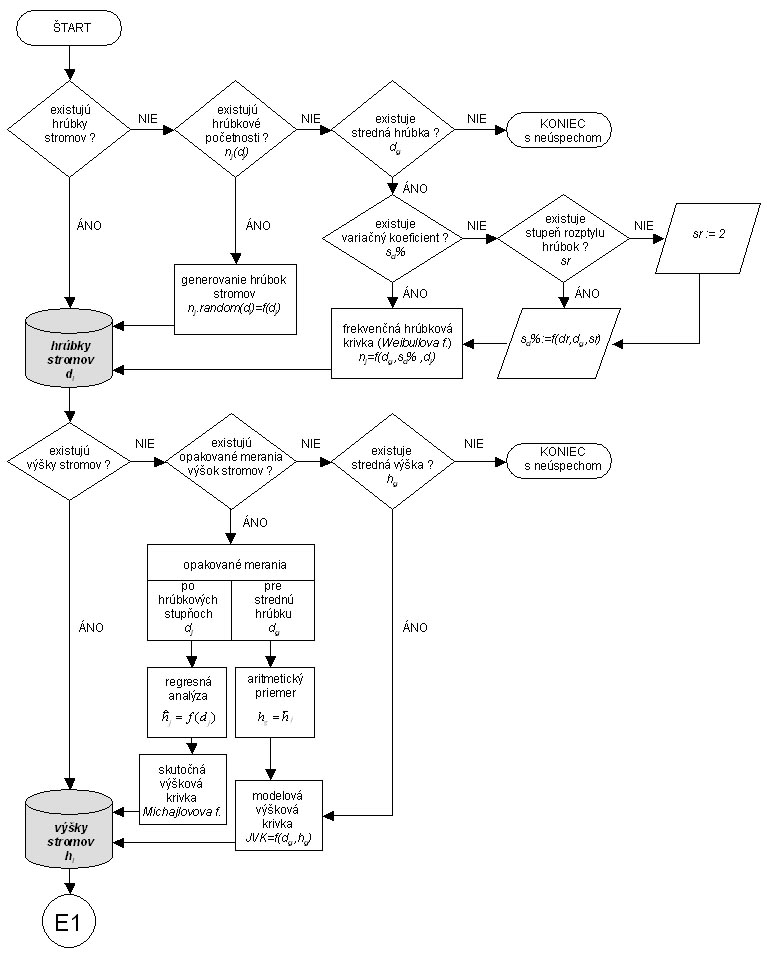
The principle of structure generation is documented in the following scheme (Fig.1 and Fig.2):

Fig.1 Scheme of forest structure generation (first part)
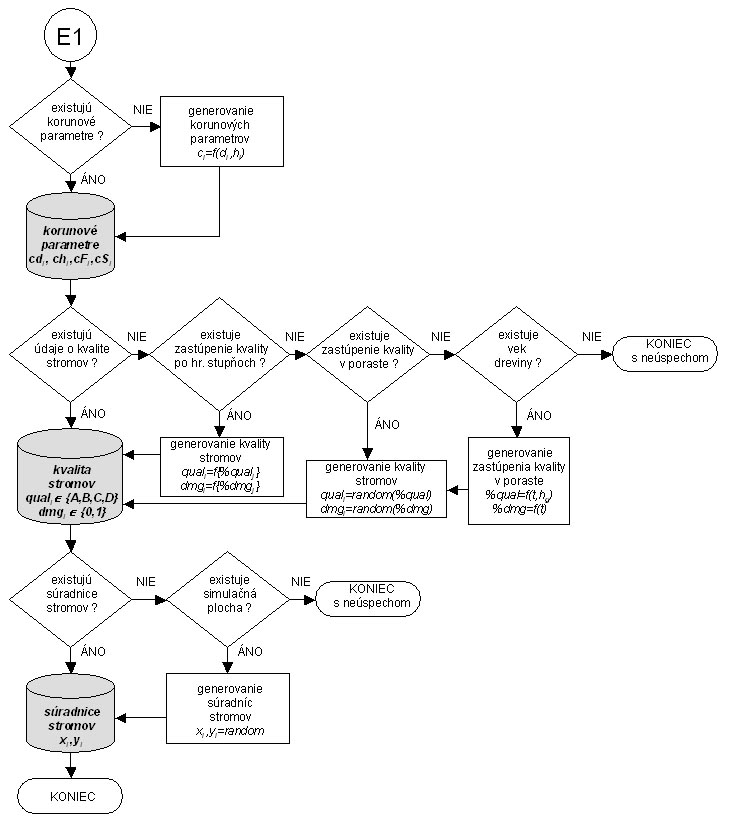
Fig.2 Scheme of forest structure generation (second part)
Generating tree diameters from diameter frequencies
|
In this case, tree diameter classes from the standard mensurational practice beginning with diameter class 10 and terminating at diameter class 90, while one diameter class is 4cm wide, are used:
up to
If the number of trees in diameter classes is known, the structure generator simulates a random tree diameter within each diameter class with uniform probability distribution. The diameter is generated repeatedly as many times as is the frequency of the diameter class (ni). |
Generating coefficient of variation of tree diameters
|
If the coefficient of variation is unknown but needed, it is derived from the regression based on the tree mean diameter dg and the variance degree sr: sd% = a0 + a1.dg + a2.sr + a3.dg.sr + a4.dg2.sr + a5.dg.sr2 The variance degree sr is a relative degree of diameter variability from interval 1 to 3, where 1 stands for minimum variability and 3 for maximum variability . By default, average degree 2 is used. Coefficient values ai are published in Fabrika (2005). |
Generating tree diameters from distribution curve
|
Fig.3 Procedure of tree diameter generation from the distribution curve
|
|
1. An initial number of trees per hectare (N) is calculated using stand volume per hectare (V) and the volume of mean stem (v) as: N = V/v, where mean stem volume is calculated from the volume equation of Petrá and Pajtík (1991) on the basis of mean diameter and mean height of the tree species in the stand. 2. Coefficients (b, c) of the diameter distribution function are calculated using mean diameter (dg) and coefficient of variation of diameters (sd%) as follows: b = a0 + a1.dg + a2.sd% + a3.dg.sd% + a4.dg2.sd% + a5.dg.sd%2 c = a0 + a1.dg + a2.sd% + a3.dg.sd% + a4.dg2.sd% + a5.dg.sd%2 The values of coefficients ai are published in Fabrika (2005). 3. Weibull distribution function is used to calculate the occurrence frequency of the tree diameter based on the initial tree number (N) and the width of the diameter class (h = 1 cm):
4. From obtained frequencies, tree diameters are derived by repeating the occurrence of a particular diameter according to its frequency. Tree diameters are coupled with tree heights that are calculated as described in the following section, and afterwards tree volumes are calculated using the volume equation by Petrá and Pajtík (1991). Total stand volume per hectare (V') is compared with the initial stand volume (V). If the input volume equals the derived one, the process of diameter generation is stopped, otherwise an iteration method is used to ensure their coincidence. The number of trees is decreased (or increased) by 1 depending on the difference between the initial and derived stand volume (i.e. a positive or a negative difference), and diameter generation is repeated starting from point 3. The principle is shown in Figure 3. |
Generating tree heights from real height curve
|
This generation is based on the data from repeated measurements of tree heights (h) distributed to diameter classes (d). In this case, measured heights are smoothed using Michajlov function:
The method is based on the calculation of coefficients a, b of the regression using the linearisation and the method of determinants:
|
Generating tree heights from uniform height curve (JVK)
|
This type of generation is based on mean height (hg) and mean diameter (dg) of a tree species and is valid only in the forest of age classes. The modul uses the mathematical model of melko et al. (1987):
|
Generating tree crown diameter and height to crown base
|
This generation is based on the model of Pretzsch (2001). The largest crown diameter in metres (cd) and the height to crown base in metres (ch) is calculated from the following regressions using tree diameter in cm (d1.3) and tree height in m (h) as input variables:
|
|
Figure 4 Crown model
|
The shape of the crown is simulated according to Pretzsch (2001). The basis of the method is that the crown radius (r) changes as the distance (x) from the top of the tree increases (Fig. 4). The crown is divided into two parts: sunlit (L) and shaded (D). The sunlit part can be in different shapes depending on a tree species; it is either conic (spruce), quadratic parabolic (fir, pine), or cubic parabolic (beech, oak). The shape of the sunlit part is controlled by the coefficient b. If this coefficient is equal to 0, then it is a cylinder; if b equals 1, it is a cone; the value 1/2 stands for quadratic paraboloid, while cubic paraboloid is represented by the value 1/3. The shaded part is always a truncated cone in shape and is the same for all tree species. The crown shape is further controlled by the coefficient a, which is a ratio between the length of the sunlit part of the crown (lL) and the total crown length (l): a=lL/l, and by the coefficient c, which is represented by the ratio of the basal crown radius (r0) to the widest crown radius (rmax): c=r0/rmax. The crown length is calculated from tree height (h) and height to crown base (ch), while maximum crown radius (rmax) is derived from the crown diameter (cd): l = h - ch rmax = cd/2 The morphological curve of the crown (cF) is then estimated by the following algorithm:
|
Calculation of the lateral area of the crown
|
Crown lateral area is calculated as follows: r0 = c . rmax lL = a . l lD = (1 - a) . l
where:
Total crown lateral area is then calculated as a sum of the sunlit and the shaded parts of the crown: cS = cSL + cSD
|
Generating the proportion of quality and damage in forest stands
|
The model is based only on age (t) and mean height (hg) of a tree species. Using these input data, the information about the proportion of qualitative classes (%qual) and the proportion of damaged trees (%dmg) in the forest stand is generated. The method is based on the relationships between age and damage, and between site class (q) and quality, that were derived for the purposes of the construction of assortment yield tables (Petrá et al. 1996) and were published in Halaj et al. (1990): %dmg = a + b . tc %qual = a + b . qc Site class (absolute height site class at the age of 100 years) is derived from the site class multi-curve diagram of yield tables (Halaj et al. 1987): q = f(t,hg) The percentage of quality is calculated separatelly for the quality class A as well as the sum of classes A+B. Class C is hence the complement on 100 per cent and class B is calculated as the difference between the sum of classes A+B and the class A. |
Generating tree quality and tree damage from stand quality and stand damage
|
This model uses the percentual proportion of quality classes and damaged trees in the whole forest stand, while as input it can either take the entered data or the data generated as described in the previous section. Afterwards, a random number is generated from uniform distribution and interval <0;100). A particular tree is assigned a quality following the stochastic principle depending on the occurrence probability of individual quality classes (%A, %B, %C):
The occurrence of tree damage is generated similarly:
|
Generating tree quality and tree damage from quality and damage of diameter classes
|
The model uses the frequency of proportion of quality classes and damaged trees in diameter classes (the result of the commercial taxation). In its nature, this model is the most detailed and hence, also the most exact. Generation follows deterministic approach. It means that quality and damage are assigned to the tree along with tree diameter generation depending on the diameter class, quality class and damage. |
How is forest stand structure of selection forests generated?
Selection forest is a forest managed by such management forms that are still rarely applied, i.e. it is a forest that comprises trees of all age classes in the same plot. It is exclusively naturally regenerated below the parent stand. Only the trees, which reach the removal dimensions, are removed, while either single-tree or group selection cutting is applied. In this case, input data are of type 8, or type 1 as described in the previous table (Table 1).
Generating tree diameters according to Liocurt
|
The model by Liocurt (1898) is based on the maximum diameter class dmax (removal dimension), its absolute frequency nmax, the curve shape quotient q <1,25;1,45> and the tree species proportion (Z%). The modelling procedure uses a geometric descending series: ni = n1 . q-(i-1) where n1 is absolute frequency of the first diameter class (2 cm). First, the sequential number of the last diameter class is calculated as follows: max = trunc [ (dmax + 2) / 4 ] where trunc is the function truncating the integer part of the remainder from division (in the cases when the entered dmax is not the middle of 4 cm diameter class). Next, absolute frequencies of the remaining diameter classes are calculated as: ni = round [ (nmax . qmax-i) . Z% / 100 ] where i is the sequential number of the diameter class (1..max). The estimated absolute frequency is assigned to the middle of the diameter class: di = 4 . i - 2 Afterwards, the procedure is the same as in the case of the data in the form of frequencies in diameter classes, i.e. in the same way as it was explained in the previous part. |
Generating tree diameters according to Meyer
|
The model by Meyer (1952) is based on tree species proportion in composition (Z%) and a model type of the selection forest (A,B,C,D,E). The basis of the method is to apply Meyer curve:
The curve simulates the number of trees in diameter classes of 1 cm width directly in absolute values for the diameter range from 1 to 90 cm. The coefficients k and alfa depend on the total number of trees per hectare N valid for 100% tree species proportion (Z%), which specifies the model type of the selection forest (A,B,C,D,E), and they are published in Fabrika (2005). |
Generating tree heights from height tariff
|
The tree height is determined from Korsuň function using the absolute height tariff (AVT):
The absolute height tariff represents an average height of the tree with the diameter of 50 cm. If AVT is unknown, it is estimated from the relative height tariff (RVT) as: AVT = d0 + d1.RVT + d2.RVT2 The relative height tariff depends on site quality, and can obtain values from the range from 1 to 20. The higher the tariff, the better the site. If neither absolute nor relative height tariff are known, so called arranging diameter dT and height hT are used. An arranging diameter is a mean stand diameter calculated a a quadratic average of tree diameters increased by 8 cm, while an arranging height is an average height of the trees with the arranging diameter. Using the arranging diameter and height, the closest curve from the height tariff diagram is chosen. All coefficents of the given relationships are published in Fabrika (2005). |
Generating tree crown parameters
|
The crown parameters of the trees forming selection forests are generated with the same set of algorithms as those used in the forest of age classes, as it was described above. |
Generating tree quality and tree damage
|
Tree quality and tree damage is generated from the proportion of quality classes and of damaged trees in the whole stand (generation procedure is described above). This information needs to be known, since in the selection forest it is not possible to derive these data from age and site classes. |
How are tree coordinates in a simulation plot generated?
The procedure to generate tree coordinates is the same for all forest types. It is performed in two steps. In the first step, stand macrostructure defined by a mutual mixture of tree species (random, group - in the form of circles or stripes) is generated. In the second step, stand microstructure is simulated by modelling the probability of trees spacing. In both steps, the procedure is fully stochastic.
Modelling stand macrostructure
Modelling is based on the spatial probability of tree species occurrence P(x,y). The result is the probability of tree occurrence at a particular point with coordinates x,y. In the modelling process, tree species are divided into the tree species with aggregated structure, and the tree species for stand filling. For aggregated tree species, the shape of groups (circles or stripes) and their number n can be defined. Circles are identified by the coordinates of their central points (Xi,Yi) in metres, and their diameters in metres, in which 95% of all trees (Di) occur. Stripes are identified by their centroids (Xi,Yi), their width, in which 95% of all trees (Di) occur, and the rotation angle on the centroid formed counterclockwise by the stripe and the positive part of axis y. In the case of fillers (filling tree species), their level of mixture with tree species in groups (slight, moderate, middle, strong, very strong, total) is defined. Spatial probability for aggregated structure is calculated with regard to the shape of elements following the methodology of Lep and Kindlmann (1987). Spatial probability of circles is determined as follows:
The probability of stripes is calculated as:
Hence, the total probability of appearance of a particular aggregated tree species is calculated as a sum of probabilities PC and PS: P'(x,y) = min { 1, PC(x,y) + PS(x,y) } The total probability of appearance of all aggregated tree species (m) is determined as:
The appearance probability of fillers is calculated as follows:
The coefficients a, b represent the level of mixture of the filling tree species with tree species that are aggregated in the groups. The values of the coefficients are given in Table 2. Table 2 Values of coefficients from the equation for calculating probability PF in relation to the level of mixture
The generation of horizontal coordinates is performed in the following steps: 1. Size of the simulation plot is determined (e.g. 0.25 ha, i.e. 50 x 50 m). 2. Random coordinates x and y are generated using uniform random distribution from the range of the width and the length of the simulation plot, e.g. <0;50> for x and y. At the same time, random number R is generated from uniform distribution and the range <0;1>. 3. Depending on the tree species, the function of spatial probability is selected (aggregated circular, aggregated striped, filling). The probability value P(x,y) is calculated in relation to coordinates x and y. If no group mixture of tree species occurs (circular or striped), the probability always equals to 1.0. 4. If the random number R is lower than or equal to the calculated probability P(x,y), tree coordinates are accepted. In addition, it is checked if the coordinates correspond with the spacing using the stochastic model of micostructre as described below. The procedure how macrostructure is generated is apparent from the following example (Figure 5).
|
|
Figure 5 Example of macrostructures in spruce-fir-beech stand |
Modelling stand microstructure
|
Figure 6 Principle of simulating microstructure |
This modul is based on the algorithms of Pretzsch (1993). First, the most probable distance to the nearest tree (r1) is calculated on the base of the distance of the generated tree to the second nearest tree (r2), and crown diameters of the generated tree (cd0), and of the first (cd1) and the second (cd2) neighbouring trees. In addition, transmission coefficients (k0, k1, k2), which characterise the crown resistance to light permeability as deifned by Ellenberg (1967), of the three trees enter this relationship. The transmission coefficient depends on tree species (beech and fir 1.0; spruce 0.8; oak 0.6; pine 0.2). The final mathematical formula is:
At the same time, the standard deviation of possible spacings is calculated as:
Afterwards, the probability that the spacing between the generated and the nearest tree (r1) occurs is estimated from the normal distribution function defined by arithmetic average (r1) and standard deviation (sr) as follows:
In the next step, random number is generated from uniform distribution within the range 0 and the occurrence probability of spacing r1. The generated random number is then compared with the occurrence probability of spacing r1. The decision if the coordinates of the generated tree are accepted or rejected is made as shown below:
The process of generating tree coordinates using the macrostructure filter is repeated until the generated tree also meets the conditions of the microstructure filter. In this way, all trees are placed in the simulation plot. |
Modelling altitudinal coordinates of trees
|
Figure 7 Derivation of altitudinal coordinates of trees
|
|
The terrain is defined by the grid of points of 5 x 5 m (so called lattices). The generator of the forest stand structure places individual trees inside this grid using the procedure described above. Altitudinal coordinate of each tree (zm) is derived from the horizontal tree coordinates (xm, ym) and altitudinal coordinates of the corners of a particular pixel (z1, z2, z3, z4) using the bilinear interpolation:
|
Š Copyright doc. Ing. Marek Fabrika, PhD.
Š Translated by Dr. Ing. Katarína Merganičová - FORIM