Aké vstupné údaje je možné použiť na generovanie štruktúry lesných porastov v rastovom simulátore SIBYLA
Rastový simulátor SIBYLA umožňuje generovať informácie o jednotlivých stromoch z rôznych údajových zdrojov, ktoré sú znázornené v Tab.1.
Tab.1 Možnosti vstupov a informačné zdroje pre generovanie štruktúry lesa
| charakter vstupných údajov | zdroje údajov |
| 1. Stromové údaje |
|
| 2. Údaje o početnosti: hrúbka - výška - kvalita |
|
| 3. Údaje o početnosti: hrúbka - výška |
|
| 4. Údaje o početnosti: hrúbka - kvalita |
|
| 5. Údaje o početnosti: hrúbka |
|
| 6. Porastové údaje |
|
| 7. Rastové tabuľky |
|
| 8. Parametre výberkového lesa |
|
Presnosť generovania štruktúry lesných porastov sa znižuje s podrobnosťou vstupných údajov, t.j. smerom zhora nadol v predchádzajúcej tabuľke.
Ako sa generuje štruktúra lesných porastov typu vekových tried ?
Les typu vekových tried je les, ktorý je obhospodarovaný v súčasnosti najčastejšie používanými formami hospodárenia, t.j. les ktorý vznikol obnovou na súvislých menších alebo väčších plochách. Plochy môžu vzniknúť odlesnením po obnovnej ťažbe alebo plošnej kalamite, kedy sa využíva umelé zalesňovanie s prípadnou prirodzenou obnovou vedľa materského porastu. Plochy môžu vzniknúť aj výrazným preriedením porastu zámernou ťažbou, napríklad v rámci podrastového hospodárenia alebo roztrúsenou náhodnou ťažbou. V tomto prípade sa používajú umelé podsadby alebo prirodzená obnova pod materským porastom. V oboch prípadoch sa výsledný les skladá zo stromov, ktoré majú na súvislej ploche v rámci danej porastovej vrstvy (etáže) vek v rozpätí jednej vekovej triedy (20 rokov). Patria tu rovnoveké porasty rovnorodé aj zmiešané, ako aj viacetážové a výstavkové porasty, vrátane porastových plantáží. V tomto prípade sa ako vstup využívajú údaje typu 1 až 7 v predchádzajúcej tabuľke (Tab.1).
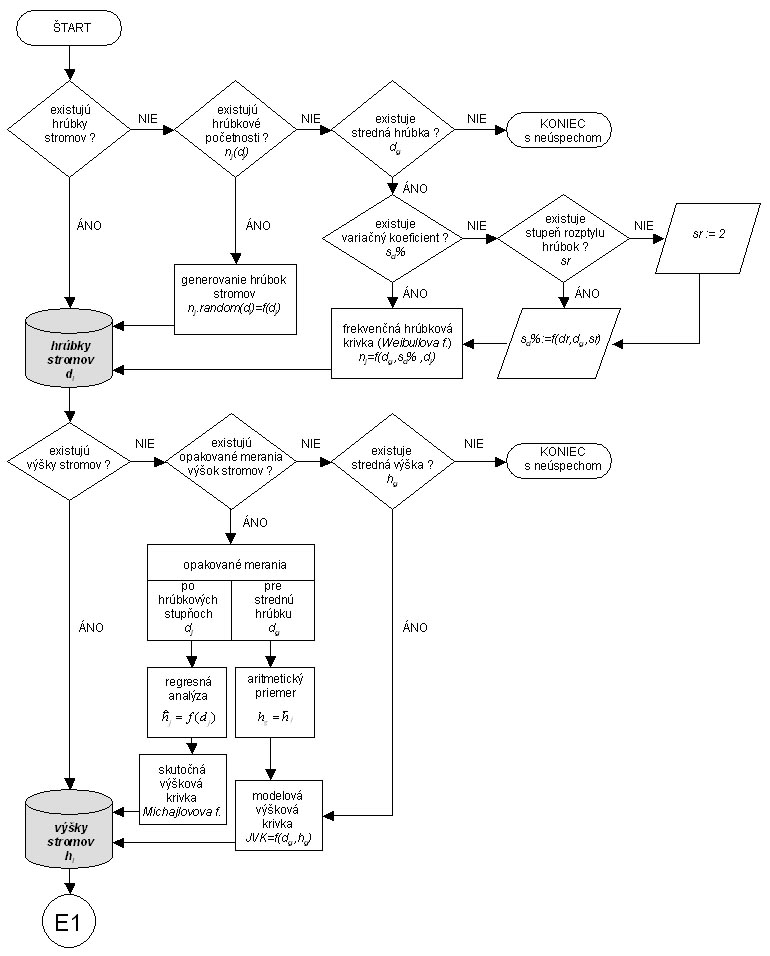
Princíp generovania štruktúry je znázornený na nasledujúcej schéme (obr.1 a obr.2):

Obr.1 Schéma generovania štruktúry lesa (prvá časť)
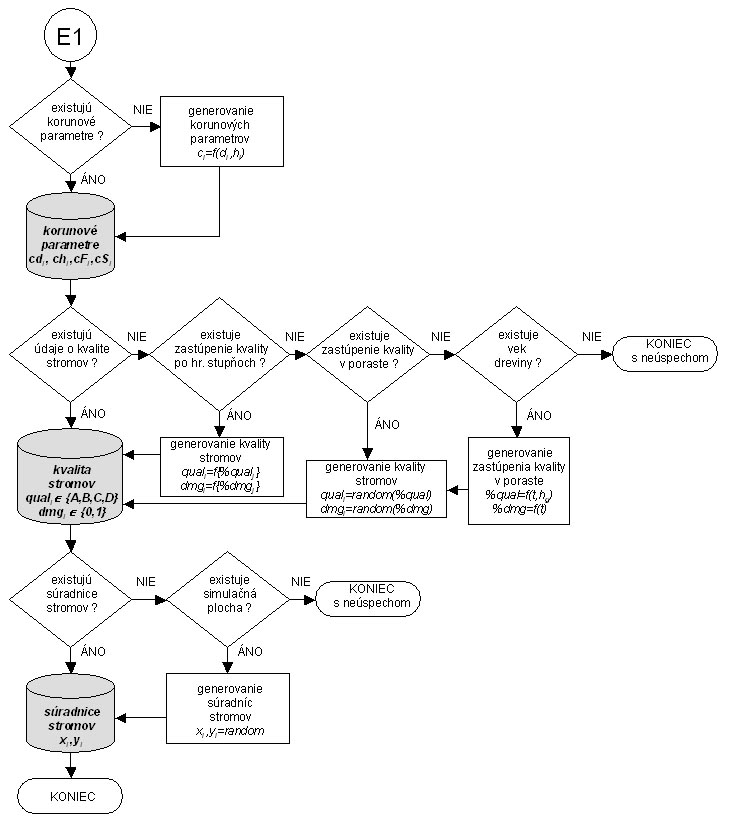
Obr.2 Schéma generovania štruktúry lesa (druhá časť)
Generovanie hrúbok stromov z hrúbkových početností
|
Používajú sa hrúbkové stupne z bežnej dendrometrickej praxe počínajúc hrúbkovým stupňom 10 a končiac hrúbkovým stupňom 90 s veľkosťou hrúbkového stupňa 4 cm:
až
V prípade ak sú známe počty stromov po hrúbkových stupňoch, tak generátor štruktúry generuje v rámci každého hrúbkového stupňa náhodnú hrúbku stromu v rámci rozpätia hrúbkového stupňa s rovnomerným rozdelením pravdepodobnosti. Hrúbka sa generuje toľkokrát, aká je početnosť v rámci hrúbkového stupňa (ni). |
Generovanie variačného koeficienta hrúbok stromov
|
V prípade ak variačný koeficient nie je neznámy a je potrebný, je odvodený z regresnej rovnice na základe strednej hrúbky dg stromu a stupňa rozptylu sr: sd% = a0 + a1.dg + a2.sr + a3.dg.sr + a4.dg2.sr + a5.dg.sr2 Stupeň rozptylu sr je relatívny stupeň variability hrúbok z intervalu 1 až 3, pričom 1 znamená minimálnu variabilitu a 3 maximálnu variabilitu. Štandardne sa používa priemerný stupeň 2. Hodnoty koeficientov ai sa nachádazajú v práci Fabrika (2005). |
Generovanie hrúbok stromov z frekvenčnej krivky
|
Obr.3 Postup generovania hrúbok stromov z frekvenčnej krivky
|
|
1. Vypočíta sa iniciálny počet stromov na hektár (N) pomocou zásoby na hektár (V) a objemu stredného kmeňa (v) podľa: N = V/v, kde objem stredného kmeňa sa vypočíta podľa objemovej rovnice Petráš a Pajtík (1991) na základe strednej hrúbky a strednej výšky dreviny v poraste. 2. Pomocou strednej hrúbky (dg) a variačného koeficienta hrúbok (sd%) sa stanovia koeficienty (b, c) frekvenčnej hrúbkovej funkcie podľa: b = a0 + a1.dg + a2.sd% + a3.dg.sd% + a4.dg2.sd% + a5.dg.sd%2 c = a0 + a1.dg + a2.sd% + a3.dg.sd% + a4.dg2.sd% + a5.dg.sd%2 Hodnoty koeficientov ai sa nachádazajú v práci Fabrika (2005). 3. Použije sa Weibullova frekvenčná funkcia na výpočet početnosti výskytu hrúbky stromu na základe iniciálneho počtu stromov (N) a veľkosti hrúbkového stupňa (h = 1 cm):
4. Pomocou získaných početností sa odvodia hrúbky stromov a to opakovaním výskytu danej hrúbky podľa jej početnosti. K hrúbkam sa dopočítajú výšky stromov podľa postupu opísaného v nasledujúcej časti a dopočítajú sa objemy stromov podľa objemovej rovnice Petráš a Pajtík (1991). Určí sa celková zásoba na hektár (V') a porovná sa so vstupnou zásobou (V). Ak sa vstupná zásoba rovná odvodenej, proces generovania hrúbok sa končí, v opačnom prípade sa použije iteračný spôsob na zabezpečenie ich zhody. Počet stromov sa zníži (resp. zvýši) o 1 strom v závislostí od rozdielu medzi vstupnou a odvodenou zásobou (t.j. kladný resp. záporný rozdiel) a proces generovania hrúbok sa opakuje od bodu 3. Princíp je zobrazený na obr.3 |
Generovanie výšok stromov zo skutočnej výškovej krivky
|
Vychádza sa z údajov opakovaných meraní výšok stromov (h) rozdelených po jednotlivých hrúbkových stupňoch (d). V tomto prípade sa skutočne namerané výšky vyrovnajú Michajlovovou funkciou:
Princíp spočíva na výpočte koeficientov a, b regresnej rovnice pomocou linearizácie a metódy determinantov:
|
Generovanie výšok stromov z jednotnej výškovej krivky
|
Vychádza sa iba zo strednej výšky (hg) a strednej hrúbky (dg) dreviny a platí iba pre les vekových tried. Model vychádza z matematického modelu podľa Šmelka et al. (1987):
|
Generovanie priemeru koruny a výšky nasadenia koruny
|
Vychádza sa z modelu Pretzscha (2001). Najširší priemer koruny v m (cd) a výška nasadenia koruny v m (ch) sa vypočíta na základe hrúbky stromu v cm (d1.3) a jeho výšky v m (h) z regresných rovníc:
|
|
Obr.4 Model koruny
|
Tvar koruny sa modeluje podľa Pretzscha (2001). Princíp spočíva na zmene polomeru koruny (r) s rastúcou vzdialenosťou (x) od vrcholu stromu (obr.4). Koruna je rozdelená na dve časti: osvetlenú (L) a zatienenú (D). Osvetlená časť má tvar kužeľa (smrek), kvadratického paraboloidu (jedľa, borovica) alebo kubického paraboloidu (buk, dub). Tvar osvetlenej časti je regulovaný prostredníctvom koeficienta b. Ak je koeficient rovný 0, tak ide o valec, ak je rovný 1, ide o kužeľ, v prípade 1/2 ide o kvadratický paraboloid a kubický paraboloid má hodnotu 1/3. Zatienená časť má u všetkých drevín tvar zrezaného kužeľa. Tvar koruny je ďalej regulovaný prostredníctvom koeficienta a, ktorý vyjadruje podiel dĺžky osvetlenej časti koruny (lL) voči dĺžke celej koruny (l): a=lL/l a koeficienta c, ktorý vyjadruje podiel bazálneho polomeru koruny (r0) k najširšiemu polomeru koruny (rmax): c=r0/rmax. Dĺžka koruny (l) sa vypočíta pomocou výšky stromu (h) a výšky nasadenia koruny (ch) a maximálny polomer koruny (rmax) sa vypočíta pomocou priemeru koruny (cd): l = h - ch rmax = cd/2 Samotná morfologická krivka koruny (cF) sa potom stanoví pomocou algoritmu:
|
Výpočet veľkosti korunového plášťa
|
Veľkosť korunového plášťa sa vypočíta podľa nasledujúceho postupu: r0 = c . rmax lL = a . l lD = (1 - a) . l
kde:
Celková veľkosť korunového plášťa sa potom vypočíta ako súčet osvetlenej a zatienenej časti koruny podľa: cS = cSL + cSD
|
Generovanie zastúpenia kvality a poškodenia v poraste
|
Model vychádza iba z veku (t) a strednej výšky (hg) dreviny. Na základe týchto vstupov sú vygenerované informácie o zastúpení tried kvality (%qual) a zastúpení poškodených stromov (%dmg) v poraste. Postup je založený na vzťahoch medzi vekom a poškodením a medzi bonitou (q) a kvalitou, ktoré boli odvodené pre účely konštrukcie sortimentačných rastových tabuliek (Petráš et al. 1996) a boli publikované v práci Halaj et al. (1990): %dmg = a + b . tc %qual = a + b . qc Bonita (absolútna výšková vo veku 100 rokov) je odvodená z bonitačného vejára rastových tabuliek (Halaj et al. 1987): q = f(t,hg) Percento kvality je počítané zvlášť pre triedu kvality A ako aj pre súčet tried A+B. Trieda C potom tvorí doplnok do 100 percent a trieda B sa vypočíta ako rozdiel medzi súčtom tried A+B a triedou A. |
Generovanie kvality a poškodenia stromov z kvality a poškodenia porastu
|
Model vychádza z percentuálneho zastúpenia tried kvality a poškodených stromov v celom poraste. Vstup môžu tvoriť zadané údaje alebo generované údaje podľa predchádzajúceho bodu. Potom sa generuje náhodné číslo z rovnomerného rozdelenia z intervalu <0;100). Kvalita sa pridelí jednotlivým stromom stochastickým princípom podľa pravdepodobnosti výskytu jednotlivých kvalitových tried (%A, %B, %C):
Podobným spôsobom sa vygeneruje aj existencia poškodenia stromu:
|
Generovanie kvality a poškodenia stromov z kvality a poškodenia hrúbkových stupňov
|
Model vychádza z početnosti zastúpenia tried kvality a poškodených stromov po hrúbkových stupňoch (výsledok priemyselnej taxácie). Model je svojou povahou najpodrobnejší a teda aj najpresnejší. Prístup generovania je deterministický. To znamená, že kvalita a poškodenie sa prideľuje zároveň s generovaním hrúbky stromu podľa jeho príslušnosti do hrúbkového stupňa, triedy kvality a poškodenia. |
Ako sa generuje štruktúra lesných porastov typu výberkového lesa ?
Výberkový les je les, ktorý sa obhospodaruje v súčasnosti zatiaľ zriedkavejšími formami hospodárenia, t.j. les ktorý ma na jednej ploche stromy všetkých vekových kategórií. Obnovuje sa výhradne prirodzeným spôsobom pod materským porastom. Odstraňujú sa stromy, ktoré dosiahli rubné dimenzie, pričom sa využíva jednotlivo stromový výberkový rub alebo skupinovite výberkový rub. V tomto prípade sa ako vstup využívajú údaje typu 8, prípadne aj údaje typu 1 v predchádzajúcej tabuľke (Tab.1).
Generovanie hrúbok stromov podľa Liocurta
|
Model podľa Liocurta (1898) vychádza z maximálneho hrúbkového stupňa dmax (dimenzie rubného typu), jeho absolútnej početnosti nmax, kvocienta tvaru krivky q <1,25;1,45> a zastúpenia dreviny (Z%). Postup modelovania vychádza z geometrického klesajúceho radu: ni = n1 . q-(i-1) kde n1 je absolútna početnosť prvého hrúbkového stupňa (2 cm). Najprv sa vypočíta poradové číslo posledného hrúbkového stupňa podľa: max = trunc [ (dmax + 2) / 4 ] kde trunc je funkcia na odrezanie celočíslenej časti zvyšku delenia (pre prípad ak sa ako dmax neudá stred 4 cm hrúbkového stupňa). Potom sa dopočítajú absolútne početností ostatných hrúbkových stupňov podľa vzťahu: ni = round [ (nmax . qmax-i) . Z% / 100 ] kde i je poradové číslo hrúbkového stupňa (1..max). Odvodená absolútna početnosť sa priradí stredom hrúbkových stupňov: di = 4 . i - 2 Ďalej sa pokračuje podobným spôsobom ako v prípade vstupných údajov vo forme početností hrúbkových stupňov, teda tak ako to bolo vysvetlené v predchádzajúcej časti. |
Generovanie hrúbok stromov podľa Meyera
|
Model podľa Meyera (1952) vychádza zo zastúpenia dreviny (Z%) a vzorového typu výberkového lesa (A,B,C,D,E). Princíp spočíva v použití Meyerovej krivky:
Krivka modeluje počet stromov pre 1 cm hrúbkové stupne priamo v absolútnych hodnotách pre rozpätie hrúbok d1.3 od 1 do 90 cm. Koeficienty k a alfa závisia od celkového počtu stromov na hektár N pri 100% zastúpení dreviny (Z%), ktorý určuje typ výberkového lesa (A,B,C,D,E) a sú opublikované v práci Fabrika (2005). |
Generovanie výšok stromov z výškovej tarify
|
Výška stromu sa určuje na základe absolútnej výškovej tarify (AVT) podľa Korsuňovej funkcie:
Absolútna výšková tarifa vyjadruje priemernú výšku stromu s hrúbkou 50 cm. Ak nie je známa určí sa na základe relatívnej výškovej tarify (RVT) podľa: AVT = d0 + d1.RVT + d2.RVT2 Relatívna výšková tarifa závisí od kvality stanovišťa a vyskytuje sa v intervale 1 až 20. Čím vyššia tarifa, tým lepšie stanovište. V prípade ak nie je známa ani relatívna výšková tarifa, tak sa použije tzv. zatrieďovacia hrúbka dT a výška hT. Zatrieďovacia hrúbka je stredná hrúbka porastu vypočítaná ako kvadratický priemer hrúbok jednotlivých stromov zväčšená o 8 cm a zatrieďovacia výška je priemerná výška stromov so zatrieďovacou hrúbkou. Na základe tejto hrúbky a výšky sa vyberie najbližšia krivka z vejára výškových taríf. Všetky koeficienty uvedených vzťahov sú opublikované v práci Fabrika (2005). |
Generovanie korunových parametrov stromov
|
Na generovanie korunových parametrov sa používa sústava algoritmov zhodná s lesom typu vekových tried, tak ako to bolo uvedené v predchádzajúcom texte. |
Generovanie kvality a poškodenia stromov
|
Na generovanie kvality a poškodenia stromov sa použije zastúpenie kvalitových tried a poškodených stromov v celom poraste, ktoré musí byť u výberkového lesa známe (postup uvedený v predchádzajúcom texte). Postup na odvodenie týchto údajov na úrovni celého porastu totižto nie je aplikovateľný, pretože vek a bonita sa u výberkového lesa nedá aplikovať. |
Ako sa generujú súradnice stromov na simulačnej ploche ?
Postup generovania súradníc stromov je zhodný pre všetky typy lesa. Prevádza sa v dvoch krokoch. P prvom kroku sa generuje makroštruktúra porastu, ktorá vyjadruje spôsob vzájomného premiešania drevín (náhodné, skupinové - vo forme kruhov alebo pásov). V druhom kroku sa modeluje mikroštruktúra na základe modelovania pravdepodobnosti odstupov stromov. Proces v oboch krokoch je plne stochastický.
Modelovanie makroštruktúry porastu
Modelovanie je založené na priestorovej pravdepodobnosti výskytu dreviny P(x,y). Výsledkom je pravdepodobnosť výskytu stromu na bode so súradnicami x,y. Dreviny sú pri modelovaní rozdelené na dreviny s agregovanou štruktúrou a dreviny porastovej výplne. Pre agregované dreviny je možné stanoviť tvar skupín s počtom n (kruhy alebo pásy). Pre kruhy sú definované stredy kruhov v metroch vo forme súradníc (Xi,Yi) a priemer kruhov v metroch, v ktorom sa vyskytuje 95% všetkých stromov (Di). Pre pásy sú definované ich stredy v metroch vo forme ťažísk (Xi,Yi), šírky pásov, v ktorých sa nachádza 95% všetkých stromov v metroch (Di) a uhol otočenia okolo ťažiska (alfai), ktorý zviera pás s kladnou poloosou y proti smeru hodinových ručičiek. Pre výpľňové dreviny sa definuje stupeň premiešania s drevinami v skupinách (slabé, mierne, stredné, silné, veľmi silné, úplné). Priestrová pravdepodobnosť pre agregovanú štruktúru sa vypočíta v závislosti od tvaru prvkov podľa metodiky Lepša a Kindlmanna (1987). Pre kruhy sa stanoví podľa:
Pre pásy sa vypočíta podľa:
Celková pravdepodobnosť výskytu agregovanej dreviny sa potom vypočíta ako súčet pravdepodobnosti PC a PS podľa: P'(x,y) = min { 1, PC(x,y) + PS(x,y) } Celková pravdepodobnosť výskytu všetkých agregovaných drevín (m) sa vypočíta podľa:
Pravdepodobnosť výskytu pre výplňové dreviny sa vypočíta podľa:
Koeficienty a, b vyjadrujú stupeň premiešania výplňovej dreviny s drevinami agregovanými v skupinách. Koeficienty sú uvedené v nasledujúcej tabuľke (Tab.2). Tab.2 Koeficienty rovnice pravdepodobnosti PF podľa stupňov premiešania
Generovanie horizontálnych súradníc súradníc prebieha podľa nasledovného postupu: 1. Určí sa veľkosť simulačnej plochy (napríklad 0,25 ha, t.j. 50 x 50 m). 2. Generuje sa náhodná súradnica x a y podľa rovnomerného náhodného rozdelenia z intervalu šírky a dĺžky strany simulačnej plochy, napr. <0;50> pre x aj y. Zároveň sa generuje náhodné číslo R z rovnomerného rozdelenia z intervalu <0;1>. 3. Zvolí sa funkcia priestorovej pravdepodobnosti patriaca danej drevine (agregovaná kruhová, agregovaná pásová, výplňová). Dopočíta sa hodnota pravdepodobnosti P(x,y) na základe súradníc x a y. Ak neexistuje žiadne skupinové premiešanie drevín (kruhové alebo pásové), vtedy má pravdepodobnosť hodnotu rovnú vždy 1,0. 4. Ak je náhodné číslo R menšie alebo rovné ako príslušná pravdepodobnosť P(x,y), potom sú súradnice stromu prijaté. Súradnice sa ešte preveria na rozostup na základe stochastického modelu mikroštruktúry podľa postupu uvedeného v nasledujúcom texte. Postup generovania makroštruktúry je zjavný z príkladu popísaného v nasledujúcom príklade (obr.5)
|
|
Obr.5 Príklad makroštruktúry smrekovo-jedľovo-bukového porastu |
Modelovanie mikrošturktúry porastu
|
Obr.6 Princíp modelovania mikorštruktúry |
Vychádza z algoritmov Pretzscha (1993). Najprv sa vypočíta najpravdepodobnejší odstup od najbližšieho stromu (r1) na základe odstupu generovaného stromu od druhého najbližšieho existujúceho stromu (r2) a priemerov korún generovaného (cd0), prvého (cd1) a druhého (cd2) stromu. Do vzťahu zároveň vstupujú transmisné koeficienty (k0, k1, k2) uvedených stromov, ktoré vyjadrujú odpor svetelnej priepustnosti koruny podľa Ellenberga (1967). Transmisný koeficient je závislý od druhu dreviny (buk a jedľa 1,0; smrek 0,8; dub 0,6; borovica 0,20). Výsledná matematická formulácia je nasledovná:
Zároveň sa vypočíta aj smerodajná odchýlka možných odstupov podľa:
Potom sa stanoví pravdepodobnosť výskytu odstupu od najbližšieho stromu (r1) z funkcie normálneho rozdelenia definovaného aritmetickým priemerom (r1) a smerodajnou odchýlkou (sr) podľa:
V ďalšom kroku sa generuje náhodné číslo s rovnomerným rozdelením z intervalu od 0 po pravdepodobnosť výskytu odstupu r1 a náhodné číslo sa porovná s pravdepodobnosťou výskytu odstupu r1. Rozhodnutie o prijatí súradníc generovaného stromu je potom nasledujúce:
Proces generovania súradníc stromu podľa filtra makroštruktúry sa opakuje dovtedy, kým generovaný strom nesplní požiadavku aj filtra mikroštruktúry. Takýmto spôsobom sú umiestnené všetky stromy na simulačnej ploche. |
Modelovanie výškových súradníc stromov
|
Obr.7 Spôsob odvodenia výškových súradníc stromov
|
|
Terén je definovaný sieťou bodov 5 x 5 m (tzv. lattices). Do tejto siete sa umiestnia generátorom štruktúry porastu jednotlivé stromy podľa postupu uvedeného v predchádzajúcom texte. Pre odvodenie výškovej súradnice každého stromu (zm) sa použije bilineárna interpolácia na základe horizontálnych súradníc stromu (xm, ym) a výškových súradníc rohov príslušnej bunky (z1, z2, z3, z4):
|
© Copyright doc. Ing. Marek Fabrika, PhD.