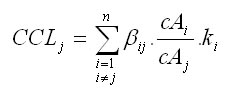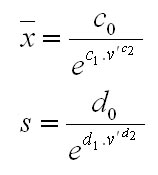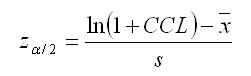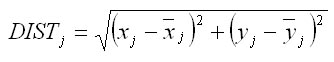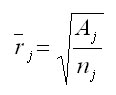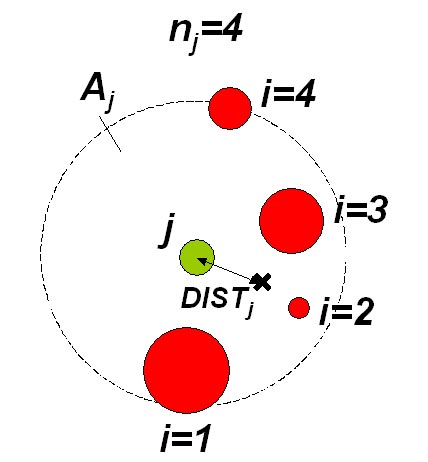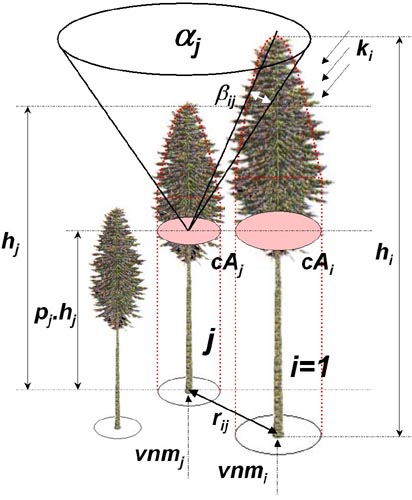
Figure 1 Principle of calculating index CCL

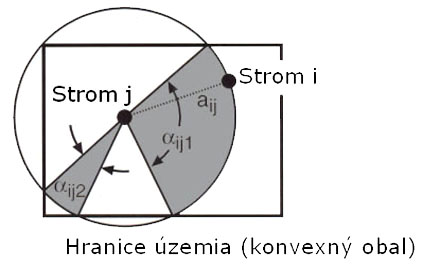
The model of crown competition for light represents the basic element of the quantification of the competition pressure of the trees. The model is based on the calculation of the index CCL (crown competition light). The principle of the index is shown in Figure 1. First, competition angles Beta_ij for each assessed tree and its potential competitors are determined. The angle Beta_ij  is based on the competition light cone, which is tree-species-specific. The cone is reversed, while its vertex is placed at a specific relative height (p) within the tree. The sides of the lateral area of the cone form a specific angle (Alfa). The parameters of the cone are published in Fabrika (2005). In the case of light-demanding tree species (pine, oak), the vertex of the cone is placed in higher parts of the stem, and the fork angle (Alfa) is greater than for shade-bearing or indifferent species (beech, fir, spruce). The angle Beta_ij is determined for the trees (competitors) with the crown occurring inside the light cone. It is defined as an angle between the lateral area of the cone and the join of the cone vertex with the top of the competitor. Figure 1 presents how the competition angle is calculated. Its magnitude can be calculated from the height of the assessed tree (h_j), elevation of the foot of the assessed tree (vnm_j), competitor tree height (h_i), elevation of the competitor treefoot (vnm_i), and the distance between the center lines of both stems (r_ij) using the trigonometrical principles:  

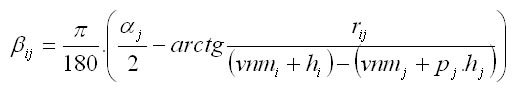
These angles (given in radian measures) are then reduced by the ratio of crown basal areas of the competitor (cA_i) to the assessed tree (cA_j) at the height of the cone vertex, and by the transmission coefficient of the competitor crown (k_i) according to Ellenberg (1963).  Afterwards, they are merged into a cumulated competition index. Transmission coefficients stand for tree-species-specific resistance to light permeability (spruce 0.8, fir 1.0, pine 0.2, beech 1.0, oak 0.6). The transmission coefficient of dead trees is equal to 0.01. Crown basal areas (cA_i, cA_j) are calculated as circle areas, while their radii are derived from crown shapes. If the light cone vertex is situated in the sunlit part of the crown, the radius is calculated using the distance between the basal area and the top of the tree for argument x:

x_i = (1 - p_j) . h_j  resp.  x_i = (vnm_i + h_i) - (vnm_j + p_j . h_j)

In cases when the light cone vertex is placed within the shaded part of the crown or below the crown, the largest tree crown radius is used. The shapes of crown basal areas are marked in Figure 1 by red dotted lines. Index CCL is equal to the sum of all angles: 

Figure 2 Principle of determining the boundaries of the sample plot (plot convex hull) 

Figure 3 Principle of correcting the edge effect using linear expansion 

In the growth simulator SIBYLA, the competition index CCL_j is also freed of the error of the edge effect. This error occurs for those trees that grow on the edge of the simulation plot. The simulation plot is only a representative sample of the original forest stand. Hence, in reality the trees on the edge of the plot are surrounded by their competitors. Using the above-mentioned calculation method, edge trees gain an advantage over the trees situated inside the sample plot. The edge effect is corrected as follows:  

1. The convex circumference of the plot is determined using the algorithm known in geometry as a convex hull (Fig. 2). The algorithm searches for the edge trees (blue dots in Fig. 2). Linking them together, a minimum convex hull is created, inside which all other trees occur (small black crosses in Fig. 2).  

2. For the correction, linear expansion according to Martin et al. (1977) is used: 

Linear expansion determines the total angle Alfa_ij for each competitor of the assessed tree. The total angle Alfa_ij is equal to the sum of the angles of the circle sectors around the assessed tree with the radius equal to the distance between the competitor and the assessed tree (a_ij), which occur inside the convex hull of the plot. An example in Figure 3 presents the sectors in grey colours. The competition angle Beta_ij is then increased (expanded) on the base of the ratio of the whole circle to the total sum of the sectors. The smaller the sectors are, the greater the expansion of the competition angle will be. The competition angle will have minimum expansion of the value 1, if the whole circle with the radius a_ij demarcated around the assessed tree occurs inside the convex hull. 

At the same time, a deviation of the competition index from average conditions is calculated. This deviation is used in other models of the simulator. From tree diameter and height, an auxiliary variable v', representing tree volume, is calculated: 

From the regression model, an average competition index (x) and a standard deviation of competition indices (s) are calculated as follows:  

Finally, the critical value z_Alfa/2 is calculated using the lognormal distribution as a deviation of the real competition index from its average value: 

The model coefficients were published in Fabrika (2005).

The shortcoming of the competition index CCL is that it does not account for the directional position of the competitors. It means that two trees can have the same value of the index CCL, if they are surrounded by the competitors of equal dimensions and distance from the assessed tree, although around one tree the competitors are evenly distributed, while around the other tree they are situated only on one side. In the second case, the actual pressure of the competitors is lower. In order to account for this effect, another algorithm described by Pukkala (1989) in Finland is used. Figure 4 presents the principle of calculating the competition assymetry. First, the coordinates of the competition centre (the cross in Figure 4) are calculated as a weighted arithmetical mean of the competitors´coordinates (x_i, y_i), while the values CCL_ij of the individual competitors are taken as weights:

The absolute distance of the competition centre is determined from the coordinates of the competition centre (x_j, y_j) and of the assessed tree (x_j, y_j) as follows: 

The absolute distance is further relativised using the average value of spacing between trees n_j in the area A_j when modelling tree distribution according to: 

The area A_j equals to the area of the circle with the radius equal to the distance to the furthest competitor. In the calculation, the number of all competitors including the assessed tree is used. The relative distance of the competition centre is then determined as: 

It is easy to interpret this value. If the competition is perfectly symmetric, the coordinates of the competition centre and of the assessed tree are equal, and the resulting value is zero. The greater the asymmetry, the larger the value of RDIST.

Fig.4 Principle of determining the competition assymetry

The model specifies the influence of tree species intermingling on the increment behaviour, which was proved in mixed spruce-beech forest stands by Kennel (1965), Petri (1966), Pretzsch (1992), Rothe (1997) and Wiedemann (1942). The principle lies in the calculation of the index MIX_j for each assessed tree according to: 

The index expresses the ratio of the total area of the crown surface of coniferous competitors (i is the element of N) to the total area of the crown surface of all trees. All trees around the assessed tree distant not more than the double crown diameter or 10 m (if the double crown diameter is less than 10m), are included in the calculation.