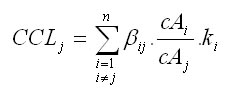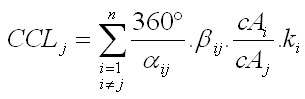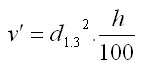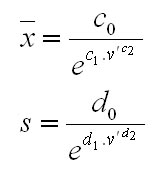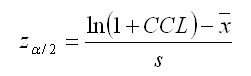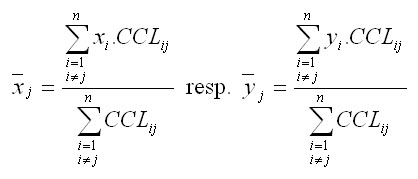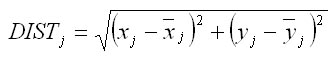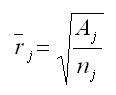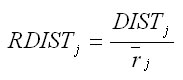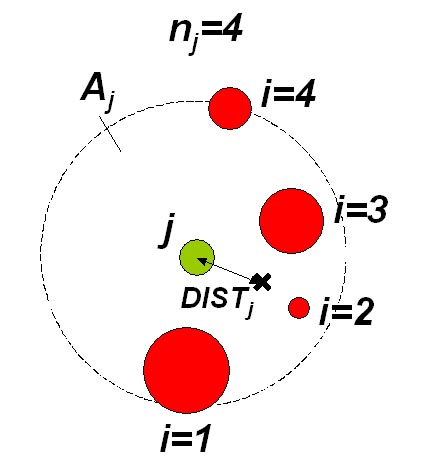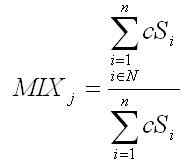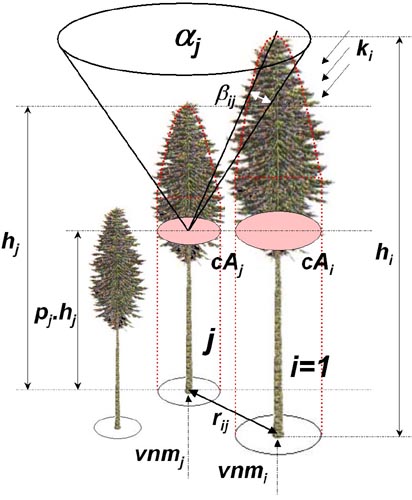
Obr.1 Princíp výpočtu indexu CCL

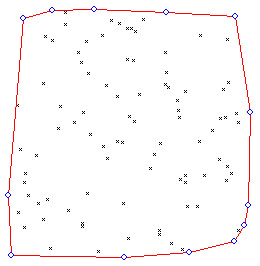
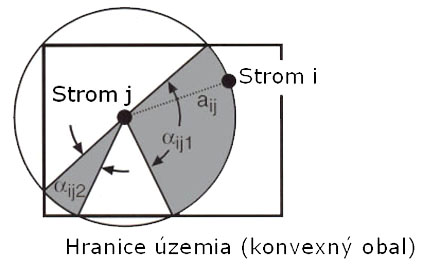
Model korunovej svetelnej konkurencie predstavuje základnú zložku pri kvantifikácií konkurenčného tlaku stromov. Model vychádza z výpočtu indexu CCL (v anglickom preklade crown competition light). Princíp indexu je znázornený na obr.1. Najprv sa stanovia konkurenčné uhly Beta_ij pre každý hodnotený strom a jeho potenciálnych konkurentov. Uhol Beta_ij vychádza z konkurenčného svetelného kužeľa, ktorý závisí od druhu dreviny. Kužeľ je obrátený hrotom dole. Vychádza z bodu v určitej relatívnej výške stromu (p). Strany obvodového plášťa zvierajú špecifický uhol (Alfa). Parametre kužeľa sú uvedené v práci Fabrika (2005). Svetlo znášajúce dreviny (borovica, dub) majú hrot kužeľa posunutý do vyšších častí kmeňa a uhol roztvorenia je väčší ako u tieň znášajúcich alebo indiferentných drevín (buk, jedľa, smrek). Uhol Beta_ij potom vzniká u tých drevín (konkurentov), ktoré v okolí hodnoteného stromu zasahujú korunou do svetelného kužeľa. Je definovaný ako uhol medzi obvodovým plášťom svetelného kužeľa a spojnicou vrcholu kužeľa s vrcholom konkurenta. Spôsob výpočtu konkurenčného uhla je zjavný z obr.1. Z trigonometrie je možné vypočítať jeho veľkosť na základe výšky hodnoteného stromu (h_j), nadmorskej výšky päty hodnoteného stromu (vnm_j), výšky konkurenta (h_i), nadmorskej výšky päty konkurenta (vnm_i) a vzdialeností medzi osami oboch kmeňov (r_ij):

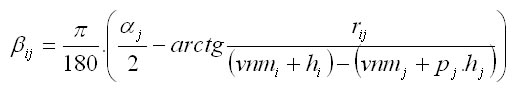
Takto stanovené uhly (v oblúkovej miere, t.j. v radiánoch) sa potom združujú do kumulovaného konkurenčného indexu, pričom sú ešte redukované pomocou pomeru medzi kruhovou základňou koruny konkurenta (cA_i) a hodnoteného stromu (cA_j) vo výške hrotu svetelného kužeľa ako aj transmisným koeficientom koruny konkurenta (k_i) podľa Ellenberga (1963). Koeficienty vyjadrujú odpor svetelnej priepustnosti v závislosti od druhu dreviny (smrek 0,8, jedľa 1,0, borovica 0,2, buk 1,0, dub 0,6). U odumretých stromov je transmisný koeficient rovný 0,01. Kruhové základne korún stromov (cA_i, cA_j) sa vypočítajú ako obsahy kruhov s polomermi, ktoré sa odvodia z tvaru koruny. V prípade, ak hrot svetelného kužeľa spadá do osvetlenej časti koruny stromu, tak sa pri výpočte polomeru za hodnotu x dosadí vzdialenosť kruhovej základne od vrcholu stromu:

x_i = (1 - p_j) . h_j  resp.  x_i = (vnm_i + h_i) - (vnm_j + p_j . h_j)

V prípade, ak hrot svetelného kužeľa spadá do zatienenej časti koruny stromu, alebo pod korunu stromu, tak sa použije najširší polomer koruny stromu. Tvary korunových kruhových základni sú na obr.1 vyznačené červenou bodkovanou čiarou. Výsledkom agregovania uhlov je index CCL:

Obr.2 Princíp určenia hraníc simulačnej plochy (konvexný obal plochy)

Obr.3 Princíp korekcie okrajového efektu pomocou lineárnej expanzie

Konkurenčný index CCL_j je v rastovom simulátore SIBYLA zbavený aj chyby z okrajového efektu. Tá vzniká u stromov, ktoré rastú na okraji simulačnej plochy. Simulačná plocha je iba reprezentatívny výrez pôvodného porastu. Stromy na jej okraji v skutočnom poraste majú konkurentov. Pri predchádzajúcom výpočte konkurenčného indexu sú tieto stromy vo výhode oproti stromom vo vnútri simulačnej plochy. Postup korekcie okrajového efektu je nasledovný:

1. Určí sa konvexný obal plochy pomocou algoritmu ktorý je v rovinnej geometrii známy pod názvom convex hull (obr.2). Algoritmus vyhľadáva okrajové stromy (modré krúžky na obr.2), ktorých pospájaním vzniká minimálny konvexný obal vo vnútri ktorého sa nachádzajú všetky ostatné stromy (malé čierne krížiky na obr.2)

2. Na korekciu sa potom použije lineárna expanzia podľa Martina et al. (1977): 

Lineárna expanzia určuje pre každého konkurenta hodnoteného stromu celkový uhol Alfa_ij, ktorý vyjadruje sumu uhlov kružnicových výsekov okolo hodnoteného stromu s polomerom rovným vzdialenosti konkurenta od hodnoteného stromu (a_ij), ktoré sa nachádzajú vo vnútri konvexného obalu plochy. V príklade na obr.3 sú kružnicové výseky znázornené sivou farbou. Konkurenčný uhol Beta_ij sa potom zväčšuje (expanduje) na základe pomeru medzi plným kruhom a celkovou sumou kružnicových výsekov. Čim menšie sú kružnicové výseky, tým väčšiu expanziu má konkurenčný uhol stromu. Minimálnu expanziu s hodnotou 1 má konkurenčný uhol, ak sa vo vnútri plochy nachádza plný kruh s polomerom a_ij okolo hodnoteného stromu. 

Zároveň sa vypočíta odchýlka konkurenčného indexu od priemerného stavu. Odchýlka sa používa v niektorých ďalších modeloch. Na základe hrúbky a výšky stromu sa vypočíta pomocná veličina v', ktorá zastupuje objem stromu:

Z regresného modelu sa dopočíta priemerný konkurenčný index (x) a smerodajná odchýlka konkurenčných indexov (s):

Napokon sa vypočíta kritická hodnota z_Alfa/2 ako odchýlka skutočného konkurenčného indexu od jeho priemernej hodnoty na základe lognormálneho rozdelenia:

Koeficienty modelu sú opublikované v práci Fabrika (2005).

Určitý nedostatok konkurenčného indexu CCL spočíva v tom, že neberie ohľad na smerovú polohu konkurentov. Rovnaký index CCL môže vzniknúť u konkurentov, ktorí majú rovnaké dimenzie a vzdialeností voči hodnotenému stromu, ale majú na jednej strane rovnomerné rozmiestnenie po obvode stromu a na druhej strane sú rozmiestnené iba z jednej strany stromu. V druhom prípade je samozrejme konkurenčný tlak reálne nižší. Preto sa využíva ďalší algoritmus, ktorý bol popísaný vo Fínsku Pukkalom (1989). Princíp vyčíslenia konkurenčnej asymetrie je znázornený na obr.4. Najprv sa vypočítajú súradnice ťažiska konkurencie (krížik na obr.4) ako vážený aritmetický priemer súradníc konkurentov (x_i, y_i), pričom ako ich váhy vystupujú hodnoty CCL_ij jednotlivých konkurentov:

Na základe súradníc ťažiska (x_j, y_j) a polohy hodnoteného stromu (x_j, y_j), sa vypočíta absolútna vzdialenosť ťažiska od stromu podľa:

Absolútna vzdialenosť je ďalej relativizovaná na základe priemerného rozostupu stromov n_j na ploche A_j pri modelovaní rozmiestnení stromov podľa:

Za plochu A_j sa považuje obsah kruhu s polomerom k najvzdialenejšiemu konkurentovi. Do výpočtu vstupuje počet všetkých konkurentov vrátane hodnoteného stromu. Relatívna vzdialenosť ťažiska sa potom vypočíta podľa:

Interpretácia takto stanovenej hodnoty je jednoduchá. V prípade, ak je konkurencia úplne symetrická, súradnice ťažiska konkurencie a súradnice hodnoteného stromu sú zhodné a výsledná hodnota je nulová. Čím väčšia je asymetria, tým vyššia je hodnota RDIST.

Obr.4 Princíp stanovenia konkurenčnej asymetrie

Model premieta účinok premiešania drevín na chovanie prírastku, ktoré bolo dokázané pre zmiešané porasty smreka a buka Kennelom (1965), Petrim (1966), Pretzschom (1992), Rotheom (1997) a Wiedemannom (1942). Princíp spočíva vo výpočte indexu MIX_j pre každý hodnotený strom podľa:

Index vyjadruje podiel celkovej plochy korunového plášťa ihličnatých konkurentov (i je prvkom N) voči celkovej ploche korunového plášťa všetkých jedincov. Do výpočtu sa berú všetky stromy v okolí hodnoteného stromu do vzdialenosti dvojnásobku priemeru jeho koruny, minimálne však 10 m.