Čo je to správnosť, presnosť a vychýlenie ?
Správnosť, presnosť a vychýlenie vyjadrujú chyby rastového simulátora, ktoré majú rôzny charakter:
Presnosť (precision) vyjadruje variabilitu okolo priemernej hodnoty. Vyjadruje tzv. náhodnú chybu (residual). Mierou presnosti je smerodajná odchýlka.
Vychýlenie (bias) vyjadruje konštantnú (stálu) odchýlku od skutočnej (cieľovej) hodnoty. Vyjadruje tzv. systematickú chybu (bias). Mierou vychýlenia je aritmetický priemer odchýlok od skutočnej hodnoty.
Správnosť (accuracy) vyjadruje variabilitu okolo skutočnej (cieľovej) hodnoty. Obsahuje náhodnú chybu (residual) a môže obsahovať aj systematickú chybu (bias). Mierou správnosti je stredná chyba. Ak neexistuje žiadna systematická chyba, tak sa správnosť zhoduje s presnosťou. Variabilita okolo skutočnej hodnoty je vtedy zhodná s variabilitou okolo priemernej hodnoty.
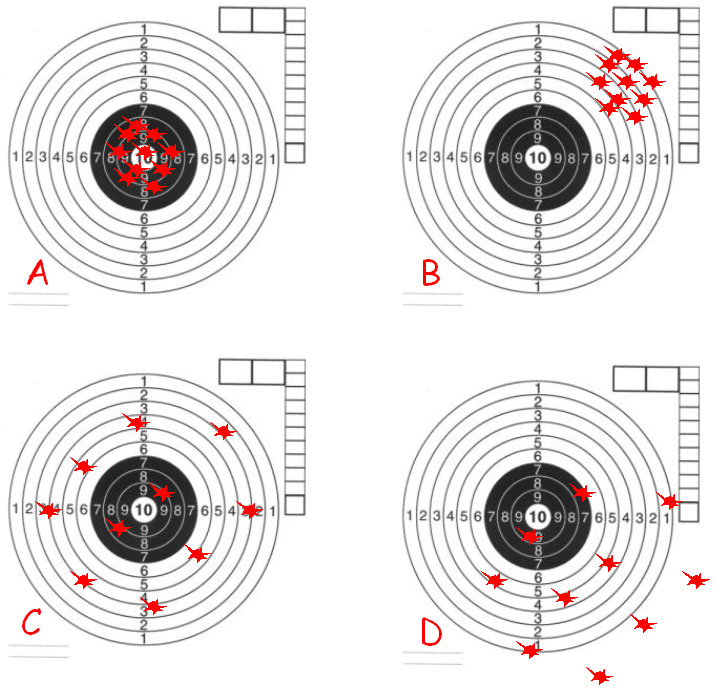
Princíp je znázornený na príklade streľby z pušky do terča (obr.1).
|
Prípad A:
|
Priemerná poloha nastrelených zásahov do terča sa zhoduje s hodnotou 10 (stred terča). Rozptyl zásahov je malý. |
|
Prípad B:
|
Priemerná poloha nastrelených zásahov do terča sa nezhoduje s hodnotou 10 (stred terča). Výrazne sa od nej odchyľuje. Odchýlke hovoríme bias. Rozptyl zásahov je malý. |
|
Prípad C:
|
Priemerná poloha nastrelených zásahov do terča sa zhoduje s hodnotou 10 (stred terča). Rozptyl zásahov je veľký. |
|
Prípad D:
|
Priemerná poloha nastrelených zásahov do terča sa nezhoduje s hodnotou 10 (stred terča). Výrazne sa od nej odchyľuje. Odchýlke hovoríme bias. Rozptyl zásahov je veľký. |

Obr.1 Vysvetlenie pojmov správnosť, presnosť a vychýlenie na príklade streľby z pušky
Ako sa preveruje empirická správnosť rastového simulátora ?
Empirická správnosť rastového simulátora sa preveruje na základe opakovaných meraní stromových údajov na trvalo fixovaných plochách. Merania vyžadujú, aby odmerané veličiny v nadväzujúcich periódach boli získane z tých istých stromov (neviditeľne alebo viditeľne očíslovaných) a aby boli zistené čo najpresnejšou metódou. Z takto získaných veličín sa vypočítajú skutočné prírastky (ireal). Z východiskovej situácie na plochách sa uskutoční simulácia na obdobie zhodné s intervalom meraní a odvodia sa modelové prírastky (imodel) stromov. Uprednostňujú sa také východiskové plochy, ktoré majú čo najviac odmeraných potrebných východiskových údajov pre rastový simulátor (hrúbky a výšky stromov, parametre korún stromov, súradnice stromov, klimatické údaje a pôdne údaje), tak aby bolo potrebné generovať čo najmenší počet východiskových charakteristík. Vypočítajú sa rozdiely medzi skutočnými prírastkami stromov a modelovými prírastkami stromov. Rozdiely spolu s modelovými prírastkami sa vynesú do grafu (obr.2) a prevedie sa regresná analýza. Regresná rovnica v grafe (červená čiara) vyjadruje systematickú chybu (bias) a variabilita okolo regresnej rovnice (zelená krivka) vyjadruje náhodnú chybu (residual).
Poznámka: modelový prírastok musí byť odvodený bez všetkých stochastických zložiek a mortalitný model musí byť zo simulácie vylúčený, pretože sa modelujú živé stromy na plochách (inventarizačných, monitorovacích alebo výskumných).
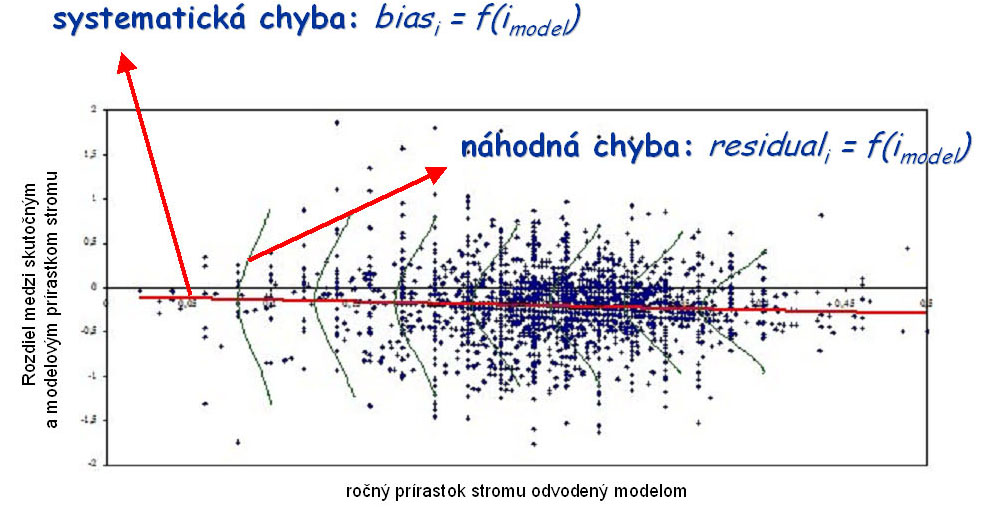
Obr.2 Princíp preverenia empirickej správnosti rastového simulátora
Ako regresnú rovnicu je možné použiť akúkoľvek vhodnú rovnicu, najčastejšie sa však používa priamka. Na obr.3 je znázornená rôzna situácia, ktorá môže nastať pri odvodzovaní systematickej chyby (obr.3):
| Prípad_A | Priamka sa zhoduje s osou x. Systematická chyba modelu neexistuje: bias = 0 |
| Prípad_B | Priamka je rovnobežná s osou x a pretína kladnú poloos y v priemernej hodnote y. Model systematicky podhodnocuje skutočnosť s rovnakou konštantne veľkou hodnotou bez ohľadu na veľkosť modelového prírastku: bias = y |
| Prípad_C | Priamka je rovnobežná s osou x a pretína zápornú poloos y v priemernej hodnote y. Model systematicky nadhodnocuje skutočnosť s rovnakou konštantne veľkou hodnotou bez ohľadu na veľkosť modelového prírastku: bias = y |
| Prípad_D | Priamka zviera s osou x nenulový uhol. Model má systematickú chybu s premenlivou hodnotou v závislosti od hodnoty modelového prírastku: biasi = f(imodel) |
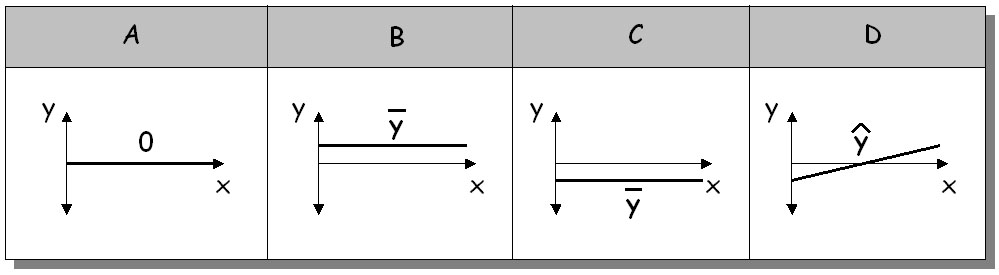
Obr.3 Rôzne prípady pri odvodzovaní systematickej chyby modelu
Pri odvodzovaní systematickej chyby v prípadoch B, C a D, je ešte potrebné previesť test pre štatistické dokázanie chyby, pretože v dátovom materiáli sa mohla vyskytnúť pod vplyvom náhodných činiteľov spôsobených výberovou vzorkou. V prípade B a C sa zväčša prevádza test významnosti odchýlky aritmetického priemeru od nuly a v prípade D sa prevádza test významnosti odchýlky korelačného koeficienta od nuly, prípadne test odchýlky absolútneho a regresného koeficienta od nuly (viď príslušná literatúra biometrie).
Pre odvodenie náhodnej chyby sa používa odlišný prístup v závislosti od charakteru kolísania hodnôt okolo regresnej rovnice. Pritom môžu nastať dva prípady (obr.4):
| homoskedasticita | Rozptyl hodnôt okolo regresnej čiary je rovnaký.
|
| heteroskedasticita | Rozptyl hodnôt sa líši pozdĺž regresnej rovnice. Ako náhodná chyba sa používa regresný vzťah medzi modelovým prírastkom a náhodnou chybou: residuali = f(imodel) |
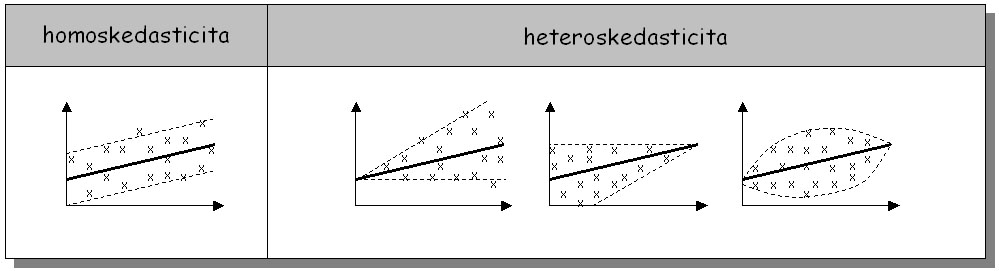
Obr.4 Rôzne prípady pri odvodzovaní náhodnej chyby modelu
Výsledná empirická správnosť rastového simulátora sa potom vypočíta podľa:
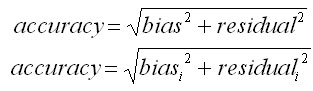
v závislosti od toho či systematická chyba a náhodná chyba je konštantná (prvý vzorec) alebo je premenlivá v závislosti od hodnoty modelového prírastku (druhý vzorec). Je to stredná chyba modelu (mean error) a vyjadruje rámec chyby, ktorý dosiahneme so 68%-nou pravdepodobnosťou. To znamená, že ak by sme opakovali simuláciu 100 krát, výsledná hodnota by bola odlišná od skutočnosti maximálne o hodnotu strednej chyby v 68 prípadoch a v 32 prípadoch by bola skutočná chyba väčšia. Ak chceme stanoviť interval chyby s 95%-nou pravdepodobnosťou, tak strednú chybu vynásobíme dvoma.
Čo je to kalibrácia rastového simulátora ?
Kalibrácia rastového simulátora je napasovanie modelu na skutočnosť reprodukciou chyby (správnosti). Používa sa postup na odvodenie správnosti simulácie podľa hore uvedeného popisu. K modelovému prírastku sa potom pripočíta reprodukovaná chyba podľa vzťahu:
ifinal = imodel + Gauss(bias,residual)
ifinal = imodel + Gauss(biasi,residuali)
v závislosti od toho či systematická chyba a náhodná chyba je konštantná (prvý vzorec) alebo je premenlivá v závislosti od hodnoty modelového prírastku (druhý vzorec). Chyba sa teda náhodne generuje na základe Gaussoveho rozdelenia, ktorého poloha je definovaná aritmetickým priemerom (bias) a smerodajnou odchýlkou (residual).
Ako je kalibrovaný rastový simulátor SIBYLA ?
|
Rastový simulátor SIBYLA bol kalibrovaný na základe opakovaných meraní trvalých monitorovacích plôch Slovenska. Kalibrovaný bol výškový (ih') a hrúbkový (id') prírastok smreka, jedle, borovice, buka a duba. Systematická chyba nebola v modeli štatisticky preukázaná. Náhodná chyba bola vyjadrená na základe regresnej priamky podľa:
Výsledný prírastok sa potom stochasticky generuje z Gaussovej krivky podľa:
Koeficienty regeresnej priamky (a, b) sú opublikované v práci Fabriku (2005). |
Ako sa vyčísľuje teoretická presnosť rastového simulátora SIBYLA ?
Rastový simulátor SIBYLA má stochastický charakter. To znamená, že ak simuláciu prevádzame pri rovnakých východiskových podmienkach a nastaveniach opakovane, zakaždým dostaneme mierne odlišné výsledky. Zdrojom náhodnosti výsledkov je predovšetkým stochastická zložka pri modelovaní prírastku hrúbky a výšky stromov ako výsledok kalibračnej techniky. Náhodnosť je však spôsobená aj inými príčinami. Celkovo možno vymenovať niekoľko zložiek rastového simulátora, ktoré majú stochastický charakter:
výpočet prírastku hrúbky stromu,
výpočet prírastku výšky stromu,
generovanie súradníc stromov,
generovanie kvality stromov,
stanovenie prirodzenej mortality stromov,
stanovenie náhleho odumretia stromov pod vplyvom škodlivých činiteľov.
Vďaka tomu môžeme vypočítať teoretickú chybu modelu ako mieru jeho presnosti. Stačí simuláciu urobiť opakovane, vypočítať aritmetický priemer zo skúmanej veličiny (napríklad zásoby) a potom vypočítať teoretickú strednú chybu:
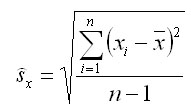
kde xi sú odlišné výsledky veličiny z opakovaných simulácií, n je počet simulácií a x je aritmetický priemer veličiny x. Táto stredná chyba vyjadruje chybu veličiny x z každej jednej simulácie (i=1..n) so 68%-nou pravdepodobnosťou, to znamená chybu ak by sme simuláciu v podobnom poraste, podmienkach a nastaveniach urobili iba raz. Výsledná chyba simulácie pri opakovanom prevedení a pri vopred stanovenej pravdepodobnosti sa potom vypočíta podľa:
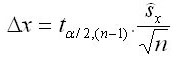
kde t je kritická hodnota podľa Studentoveho t-rozdelenia (pri 95%-nej pravdepodobnosti cca 2,00). Pri praktickom prevedení simulácie s väčšou dôležitosťou odporúčame vykonať simuláciu pre rovnaké východiskové podmienky a nastavenia minimálne 36 krát. Optimálne 6 krát zopakovať generovanie štruktúry a 6 krát opakovať prognózu (spolu 36 opakovaní). Výsledná hodnota bude potom aritmetický priemer veličiny z opakovaných simulácií x. Celková stredná chyba tejto priemernej hodnoty je potom 6 krát menšia ako stredná chyba jedinej simulácie.
Určiť strednú chybu simulácie, ktorá by bola všeobecne použiteľná, je na rozdiel od rastových tabuliek nemožné. Stredná chyba, totižto závisí od mnohých faktorov. Z najdôležitejších možno spomenúť nasledovné:
zdroj údajov pre generovanie štruktúry,
zložitosť generovanej štruktúry,
dĺžka periódy,
použitie kalamitného modelu,
výsledná charakteristika zo simulácie.
Ak za zdroj údajov použijeme údaje z trvalých výskumných plôch so známymi stromovými údajmi, stredná chyba simulácie bude menšia ako z menej presných údajov, ako sú napríklad sumárne porastové údaje, údaje rastových tabuliek alebo popis výberkového lesa. Ak sa simulácia prevádza pre rovnoveký, rovnorodý porast s jednoduchou porastovou výstavbou, stredná chyba simulácie bude menšia ako u porastov so zložitejšou štruktúrou, ako sú napríklad zmiešané etážovité alebo nerovnoveké lesy, prípadne výberkové lesy. Čím dlhšia je rastová simulácia, tým väčšia je jej stredná chyba. Ak pri simulácií aktivujeme aj kalamitný model, presnosť simulácie sa znižuje. Aj výsledná charakteristika na ktorú zameriame svoju pozornosť ovplyvňuje strednú chybu simulácie. Chyba charakteristiky jednotlivého stromu je omnoho väčšia ako chyba strednej alebo sumárnej porastovej charakteristiky. V rámci porastových charakteristík je chyba strednej výšky a strednej hrúbky najmenšia. Chyba agregovaných veličín je väčšia, napríklad chyba objemu stredného kmeňa, ale tá je stále menšia ako chyba hektárovej zásoby, pretože tá v sebe obsahuje aj chybu počtu stromov pod vplyvom stochastického mortalitného modelu.
Pri orientačnom stanovení strednej chyby sme sa zamerali na hektárovú zásobu pri dĺžke periódy 50 rokov bez použitia kalamitného modelu. Stredná chyba jednotlivej simulácie je znázornená v nasledujúcej tabuľke:
| typ simulácie | stredná chyba (68%-ná pravdepodobnosť) | chyba pri 95%-nej pravdepodobnosti |
| rovnoveký rovnorodý porast generovaný z trvalých výskumných plôch so zmeranými súradnicami a stromovými údajmi | ±2,5% | ±5% |
| rôznorodý porast s etážovitou výstavbou generovaný z porastových údajov | ±7,5% | ±15% |
| výberkový les generovaný z popisu výberkového lesa | ±15% | ±30% |
Pre porast druhého typu (rôznorodý s etážovitou výstavbou generovaný z porastových údajov) bola preverená aj chyba strednej hrúbky [±4% (so 68% pravdepodobnosťou), ±8% (s 95% pravdepodobnosťou)] a strednej výšky [±3% (so 68% pravdepodobnosťou), ±6% (s 95% pravdepodobnosťou)].
Ako sa zhoduje rastový model SIBYLA s rastovými tabuľkami ?
Rastové tabuľky tvoria normu pre produkciu rovnovekých rovnorodých porastov. Preto porovnanie rastového simulátora s rastovými tabuľkami pri rovnakých východiskových údajoch je tiež jeden z nástrojov na preverenie rastového simulátora. Rastový simulátor umožňuje prognózovať vývoj omnoho väčšej škály porastových štruktúr ako rastové tabuľky. Mal by však dokázať prognózovať vývoj rovnovekých rovnorodých porastov s podobným výsledkom ako rastové tabuľky. Rastový simulátor SIBYLA bol preverený aj týmto spôsobom. Postup bol nasledovný:
Boli generované východiskové porasty smreka, jedle, borovice, buka a duba s vekom 30 rokov pre najhoršiu, prostrednú a najlepšiu bonitu a priemernú zásobovú úroveň. Na generovanie bol použitý postup generovania z opisu porastov rastových tabuliek. Generovanie štruktúry bolo opakované vždy 6 krát.
Boli nastavené podrobné charakteristiky ovzdušia, klímy a pôdy tak, aby bol vývoj hornej porastovej výšky zhodný s vývojom hornej porastovej výšky príslušnej bonity rastových tabuliek.
Bol nastavený prebierkový režim tak, aby kopíroval prebierky v rastových tabuľkách. Bola nastavená 5 ročná perióda prebierok. Bola zvolená neutrálna prebierka so silou kopírujúcou vývoj zásoby hlavného porastu podľa rastových tabuliek.
Bola prevedená rastová simulácia s aktivovaným mortalitným modelom, stochastickou zložkou a korekciou okrajového efektu, bez použitia kalamitného modelu. Rastová simulácia bola opakovaná vždy 6 krát a bola prevedená na obdobie 100 rokov.
Boli vypočítané priemerné hodnoty vývoja zásoby pre združený a hlavný porast z 36 opakovaní simulácie (6 štruktúr x 6 prognóz). Hodnoty boli vynesené do grafov spolu s hodnotami z rastových tabuliek a boli podrobené vzájomnému porovnaniu.
Vývoj zásoby podľa rastového simulátora SIBYLA a rastových tabuliek (Halaj et al. 1987) sa u všetkých drevín a bonít dobre zhoduje. Prejavila sa však rovnaká tendencia takmer vo všetkých prípadoch. Zhruba 40 rokov sa vývoj zásoby takmer úplne zhoduje. Neskôr však SIBYLA vykazuje mierne vyššie celkové bežné prírastky. Táto tendencia je znázornená na obr.5 a obr.6 na príklade smreka a buka pre stredné bonity. Diferencia však nie až taká výrazná a teda možno povedať, že rastový simulátor SIBYLA dokáže reprodukovať aj vývoj porastov zhodný s rastovými tabuľkami a teda ich pre rovnoveké rovnorodé porasty nahradiť.
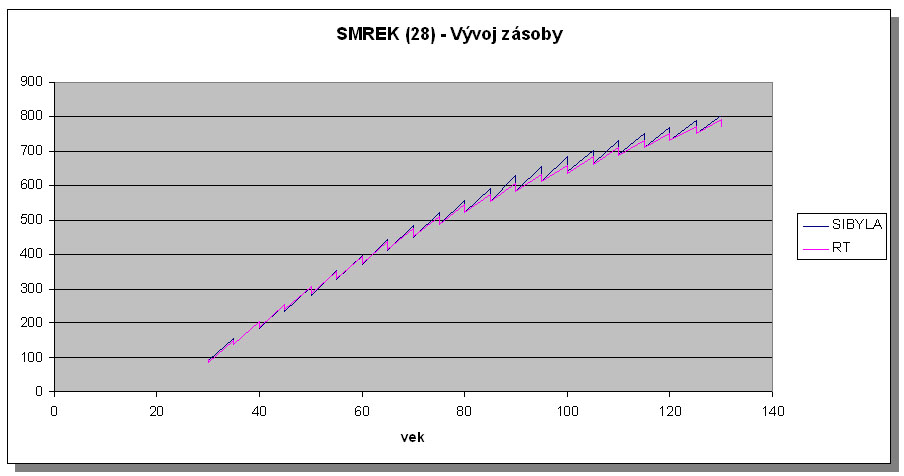
Obr.5 Porovnanie rastového simulátora SIBYLA a slovenských rastových tabuliek (RT) na príklade smreka a bonity 28
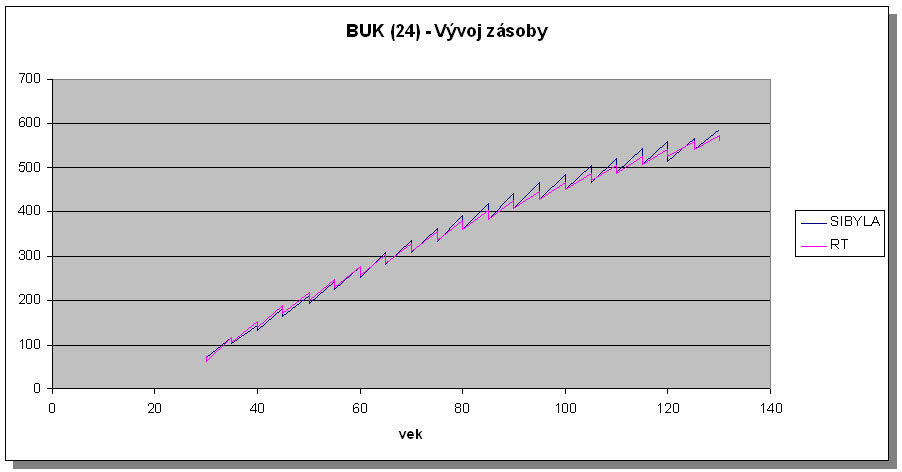
Obr.6 Porovnanie rastového simulátora SIBYLA a slovenských rastových tabuliek (RT) na príklade buka a bonity 24
© Copyright doc. Ing. Marek Fabrika, PhD.